L’enveloppe convexe d’un ensemble de points est le plus petit polygone convexe contenant tous les points. Dans cet article, nous allons implémenter un calcul d’enveloppe convexe à l’aide de l’algorithme de Graham scan, un algorithme efficace pour résoudre ce problème, puis ajouterons une approximation de la plus petite boîte englobante (OMBB).

1. Génération de points aléatoires

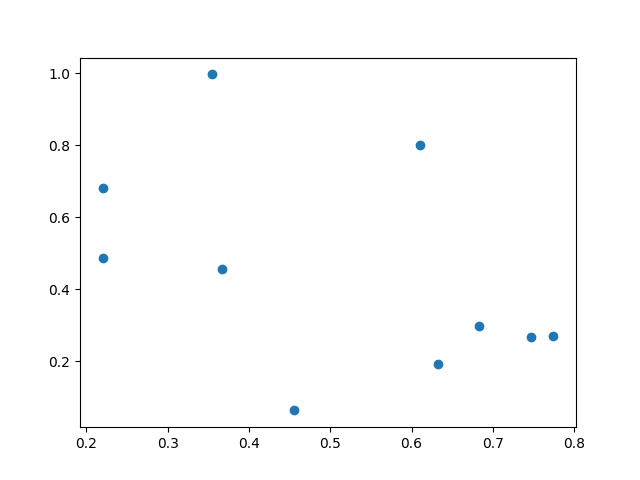
Pour commencer, nous générons un ensemble de 10 points aléatoires via numpy :

def generate_random_points():
    x = np.random.rand(10)
    y = np.random.rand(10)
    return x, y

Que l’on va visualiser avec matplotlib :

plt.scatter(x, y)
plt.show()

2. Produit vectoriel pour déterminer l’orientation

L’algorithme Graham scan utilise le produit vectoriel pour savoir si trois points sont tournés dans le sens horaire ou anti-horaire. Voici la fonction qui calcule ce produit :

def cross_product(a, b, c):
    return (b[0] - a[0]) * (c[1] - a[1]) - (b[1] - a[1]) * (c[0] - a[0])

Le résultat de cette fonction nous permet de savoir si le point c est à gauche ou à droite de la ligne définie par a et b.

3. L’algorithme de Graham scan

L’algorithme de Graham scan est utilisé pour trouver l’enveloppe convexe. Pour plus de détails, vous pouvez consulter cet article sur Wikipedia. Voici le déroulement de l’algorithme dans le code :

def convex_hull(x, y):
    # Trouver le point le plus bas (ou le plus à gauche en cas d'égalité)
    lowest = 0
    for i in range(1, len(y)):
        if y[i] < y[lowest] or (y[i] == y[lowest] and x[i] < x[lowest]):
            lowest = i

    # Trier les points par l'angle formé avec le point de référence (le plus bas)
    angles = np.arctan2(y - y[lowest], x - x[lowest])
    sorted_indices = np.argsort(angles)
    x = x[sorted_indices]
    y = y[sorted_indices]

    # Construction de l'enveloppe convexe
    stack = [0, 1]
    for i in range(2, len(x)):
        while len(stack) > 1 and cross_product((x[stack[-2]], y[stack[-2]]),
                                               (x[stack[-1]], y[stack[-1]]),
                                               (x[i], y[i])) <= 0:
            stack.pop()
        stack.append(i)

    stack.append(0)  # Retour au point de départ

    return x[stack], y[stack]

L’idée derrière cet algorithme est la suivante : tout d’abord les points sont triés en fonction de leur angle avec le premier point et l’axe des abscisses. Les deux premiers points sont ajoutés, puis pour tous les autres points, la convexité est vérifiée à l’aide du produit en croix. Si le polygone formé n’est pas convexe, les points sont enlevés.

4. Visualisation de l’enveloppe convexe

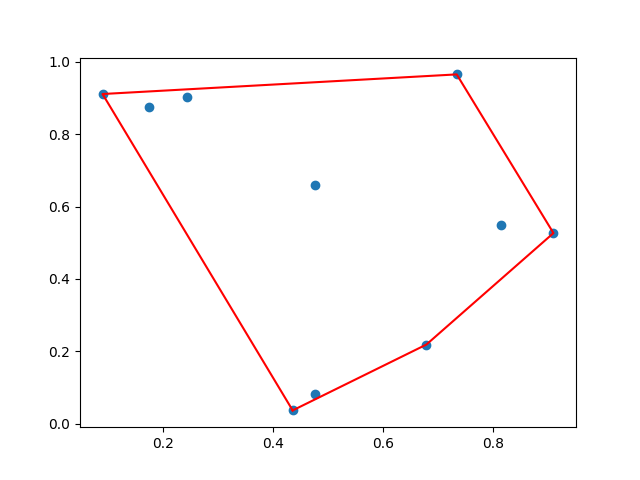
Nous visualisons les points et leur enveloppe convexe à l’aide de matplotlib :

plt.scatter(x, y)
plt.plot(x_hull, y_hull, 'r')
plt.show()

5. Calcul de la plus petite boîte englobante (OMBB)

La fonction suivante calcule l’Oriented Minimum Bounding Box (OMBB) en tournant l’enveloppe convexe autour de chaque bord pour trouver l’orientation qui minimise l’aire de la boîte englobante :

def OMBB(x_hull, y_hull):
    min_area = float('inf')
    min_rect = None
    angle = 0
    min_point = None

    for i in range(len(x_hull)):
        A = [x_hull[i], y_hull[i]]
        B = [x_hull[(i+1) % len(x_hull)], y_hull[(i+1) % len(x_hull)]]
        AB = np.array(B) - np.array(A)
        angle_AB = np.arctan2(AB[1], AB[0])

        # Rotation des points
        x_rot = x_hull * np.cos(angle_AB) - y_hull * np.sin(angle_AB)
        y_rot = x_hull * np.sin(angle_AB) + y_hull * np.cos(angle_AB)

        # Calcul des limites et de l'aire
        min_x = np.min(x_rot)
        max_x = np.max(x_rot)
        min_y = np.min(y_rot)
        max_y = np.max(y_rot)
        area = (max_x - min_x) * (max_y - min_y)
        if area < min_area:
            min_area = area
            min_rect = [[min_x, min_y], [max_x, min_y], [max_x, max_y], [min_x, max_y]]
            angle = angle_AB
            min_point = A

    min_rect = np.array(min_rect)
    min_rect = min_rect @ np.array([[np.cos(angle), -np.sin(angle)], [np.sin(angle), np.cos(angle)]])
    min_rect = np.vstack((min_rect, min_rect[0]))

    return min_rect, angle

Cette fonction tourne la boîte autour de chaque bord pour minimiser l’aire totale de la boîte. Pour chaque segment et orientation choisie, le plus petit rectangle englobant non orienté est retenu. Le plus petit d’entre tous est finalement orienté avec l’angle du segment choisi.

6. Visualisation de la boîte englobante

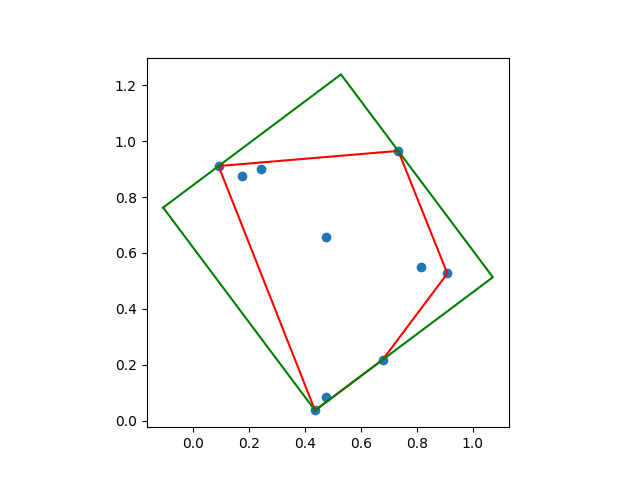
Nous affichons la boîte englobante sur les points et l’enveloppe convexe :

plt.plot(min_rect[:, 0], min_rect[:, 1], 'g')
ax = plt.gca()
ax.set_aspect('equal', adjustable='box')
plt.show()

Conclusion

Dans cet article, nous avons implémenté et expliqué l’algorithme de Graham scan pour calculer l’enveloppe convexe d’un ensemble de points, ainsi qu’une approximation de la plus petite boîte englobante. Ces techniques sont largement utilisées dans des applications de géométrie computationnelle, de vision par ordinateur, et dans des systèmes d’analyse de données.